on
Summary of Resnet Paper
In this blog, for my notes as well as for the reference of others, I have written a small summary of the paper.
About Paper
- Resnet paper title: Deep Residual Learning for Image Recognition
- Paper submission date: 10th dec 2015.
Achievements of the paper
In ImageNet competition 2015, authors secured
- First place in the classification (3.57% top-5 error on the ImageNet test set)
- First place in the localisation
- First place in the detection
In COCO competition 2015, authors secured
- First place in the detection
- First place in the segmentation
Key Contributions
- Introduced a deep residual learning framework to ease the training of deep networks.
- Showed that extreme deep residual nets are easy to optimize, but the counterpart “plain” nets (that simply stack layers) exhibit higher training error when depth increases
- Also showed that our deep residual nets can easily enjoy accuracy gains from greatly increasing depth, producing results substantially than the networks used previously
Deep residual learning framework
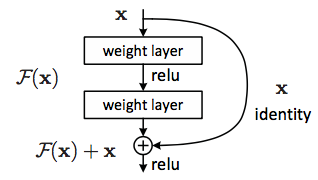
Residual learning: a building block
The idea behind the above block is, instead of hoping each few stacked layers directly fit a desired underlying mapping say \(H(x)\), we explicitly let these layers fit a residual mapping i.e.. \(F(x) = H(x) - x\). Thus original mapping \(H(x)\) becomes \(F(x) + x\).
Shortcut connections
These connections are those skipping one or more layers. \(F(x) + x\) can be understood as feedforward neural networks with “shortcut connections”.
Why deep residual framework?
The idea is motivated by the degradation problem (training error increases as depth increases). Suppose if the added layers can be constructed as identity mappings, a deeper model should have training error no greater than its shallower counterpart.
If identity mappings are optimal, it is easier to make \(F(x)\) as 0 than fitting \(H(x)\) as \(x\) (as suggested by degradation problem).
Results
In this section, we see the performance of residual networks. The models were trained on the 1.28 million training images, and evaluated on the 50,000 validation images. The performance of the networks were evaluated using top-1 error rate.
In the below table, two types of network are mentioned.
Plain Networks.
The deeper neural networks are constructed by stacking more layers on one another without shortcut connections.
ResNet.
This network architecture is based on the deep residual framework, which uses short cut connections. ResNet-X means Residual deep neural network with X number of layers, for example: ResNet-101 means Resnet constructed using 101 layers
The numbers in the table are top-1 error rates (in %) resulted when the models were tested on the ImageNet validation data.
| No of layers | Plain | ResNet |
|---|---|---|
| 18 layers | 29.94 | 27.88 |
| 34 layers | 28.54 | 25.03 |
| 50 layers | - | 22.85 |
| 101 layers | - | 21.75 |
| 152 layers | - | 21.43 |
From the above table, it is evident that resnet with more number of layers has better performance.