Summary of BatchNorm paper

Paper

• Title: Batch Normalization- Accelerating Deep Network Training by reducing Internal Covariance Shift (BN)
• Submission date: 11 Feb 2015

Achievments

• Batch Normalization (BatchNorm) achieved the same accuracy as the previous state-of-the-art image classification models with 14 times fewer training steps.
• Using the ensemble of batch normalized networks, the best published result on image classification was improved, reaching 4.9% top-5 validation error and 4.8% test error.

Key Contributions

• Identified internal Covariance Shift problem and addressed this issue by normalizing layer inputs.
• Presented novel method called BatchNorm for dramatically accelerating the training of deep networks.

Internal Covariance Shift

When the input distribution to a learning systems changes, it is known as covariance shift. This concept can be extended beyond the learning system as a whole to its parts, such as a sub-network or layer. This change in the distribution of sub-network activations (i.e. inputs to a layer) due to the change in network parameters (of preceding layers) is called Internal covariance shift. This slows down the deep neural network training by requiring:

• Lower learning rate
• Careful parameter initialization
• And this makes the network notoriously hard to train models with saturating nonlinearities.

BatchNorm

To improve the training processes, we seek to reduce the internal covariance shift. The authors proposed a new mechanism called Batch Normalization (BatchNorm), which reduces internal covariate shift and dramatically accelerates the training of deep neural nets. It accomplishes this via a normalization step that fixes the mean and variance of the layer $l$, computed for each mini-batch, to parameters $\beta_l$ and $\gamma_l$ respectively. These parameters in turn are learnt by gradient descent. BatchNorm also has a beneficial effect on the gradient flow through the network, by reducing the dependence of gradients on the scale of the parameters or of their initial values.

Advantages of BatchNorm include:

• SGD can have higher learning rates
• Can be less careful about initialization
• Also acts as a regularizer, in some cases eliminating the need for Dropout.
• BatchNorm makes it possible to use saturating nonlinearities by preventing the network from getting stuck in the saturated modes
• BatchNorm adds only two extra parameters per activation, and in doing so preserves the representation ability of the network

Experiments

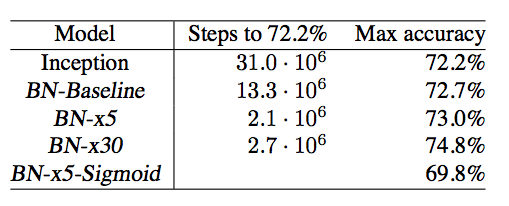
Various experiments were conducted to understand the accelerating effect of batchnorm on deep neural networks. The experiments were done using single-network classification trained on the ImageNet 2012 training data, and tested on the validation data.

• Inception: The modified inception network for image classification trained with the initial learning rate of 0.0015
• BN-Baseline: Inception with BatchNorm before each nonlinearity.
• BN-x5: Inception with BatchNorm and initial learning rate was increased by a factor of 5
• BN-x30: Similar to BN-x5, but the factor is 30
• BN-x5-Sigmoid: Like BN-x5, but with sigmoid non-linearity instead of RELU.

The ensemble of 6 BN-x30 classification networks improved over the previous state-of-the-art results.

The goal of BatchNorm is to achieve a stable distribution of activation values throughout the training. Authors applied it before the nonlinearity since that is where fixing the first and second moments is more likely to result in a stable distribution.