Introduction to Graph theory

Why Graph Theory?

Graphs are the data structure used in the study of Graph neural networks (GNNs). The fundamental graph theory is important in understanding of GNN. Therefore lets explore graph theory in detail.

Basic Representation of the Graph

• A graph is often denoted by $G = (V,E)$, where V is the set of vertices and E is the set of edges.
• An edge $e = u,v$ has two endpoints u and v, which are joined by e. Here u is called a neighbor of v, we can say that u and v are adjacent.
• An edge can be directed or undirected. Based on the type of edge, graph can be called as directed or undirected graph

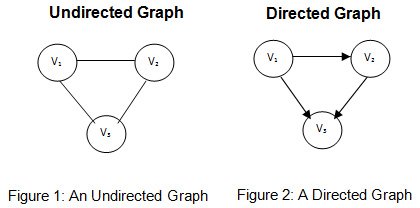
• The degree of vertice $v$ is denoted by $d(v)$, where $d(v)$ is the number of edges connected with $v$

Algebra Representation of the Graph

Adjacency matrix

• For a graph $G = (V, E)$ with $n$-vertices, it can be described by an adjacency matrix $A \in R^{n \times n}$, where

\[A_{ij}=\begin{cases} 1 & \text{if $\{v_i, v_j\} \in E$ and $i \ne j$},\\ 0 & \text{otherwise}. \end{cases}\]

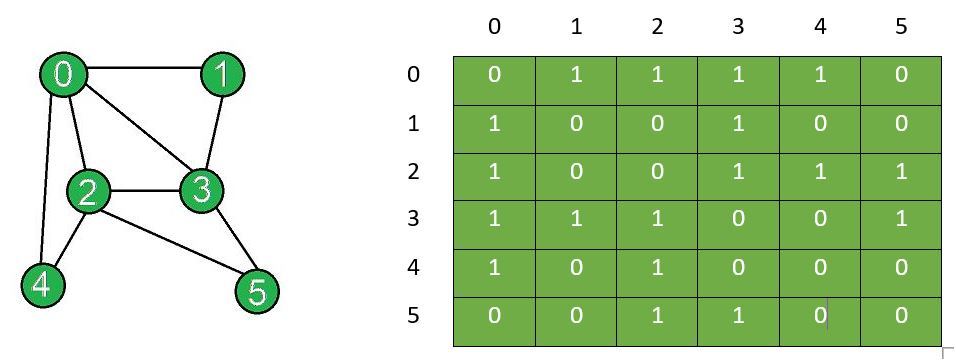Figure3: Adjacency matrix

• If a graph is undirected then its adjacency matrix is symmetric

Degree matrix

• For a graph $G = (V, E)$ with $n$-vertices, its degree matrix $D \in R^{n \times n}$ is a diagonal matrix, where

\[D_{ii} = d(v_i), \\ D_{ij} = 0 \text{ where $i \ne j$}.\]

Incidence matrix

• For a directed graph $G = (V, E)$ with $n$-vertices and $m$-edges, its incidence matrix is $M \in R^{n \times m}$, where

\[M_{ij}=\begin{cases} 1 & \text{$\exists k$ $s.t$ $e_j = \{v_i, v_k\}$},\\ -1 & \text{$\exists k$ $s.t$ $e_j = \{v_k, v_i\}$},\\ 0 & \text{otherwise}. \end{cases}\]

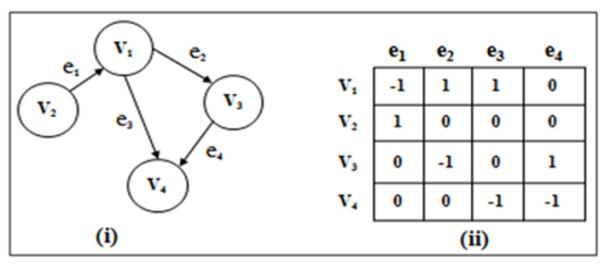Figure4: Incidence matrix

Laplacian matrix

• For a undirected graph $G = (V, E)$ with $n$-vertices, its Laplacian matrix $L \in R^{n \times n}$ is defined as

\[L = D - A.\]

• And elements of L are

\[L_{ij} = \begin{cases} (v_i) & \text{if $i = j$},\\ -1 & \text{if $\{v_i, v_j\} \in E$ and $i \ne j$},\\ 0 & \text{otherwise}. \end{cases}\]

Symmetric normalized Laplacian

• The symmetric normalized Laplacian is defined as

\[L^{sym} = D^{-1/2}LD^{-1/2}\\ \qquad\qquad = I - D^{-1/2}AD^{-1/2}.\]

• And elements of $L^{sym}$ are

\[L_{ij}^{sym} = \begin{cases} 1 & \text{if $i = j$ and $d(v_i) \ne 0$},\\ -\frac{1}{\sqrt{d(v_i)d(v_j)}} & \text{if $\{v_i, v_j\} \in E$ and $i \ne j$},\\ 0 & \text{otherwise}. \end{cases}\]

Random walk normalized Laplacian

• The random walk normalized Laplacian is defined as:

\[L^{rw} = D^{-1}L = I - D^{-1}A.\]

• And elements of $L^{rw}$ are

\[L_{ij}^{rw} = \begin{cases} 1 & \text{if $i = j$ and $d(v_i) \ne 0$},\\ -\frac{1}{d(v_i)} & \text{if $\{v_i, v_j\} \in E$ and $i \ne j$},\\ 0 & \text{otherwise}. \end{cases}\]

In the next blog we will explore more about Graph neural networks (GNN).